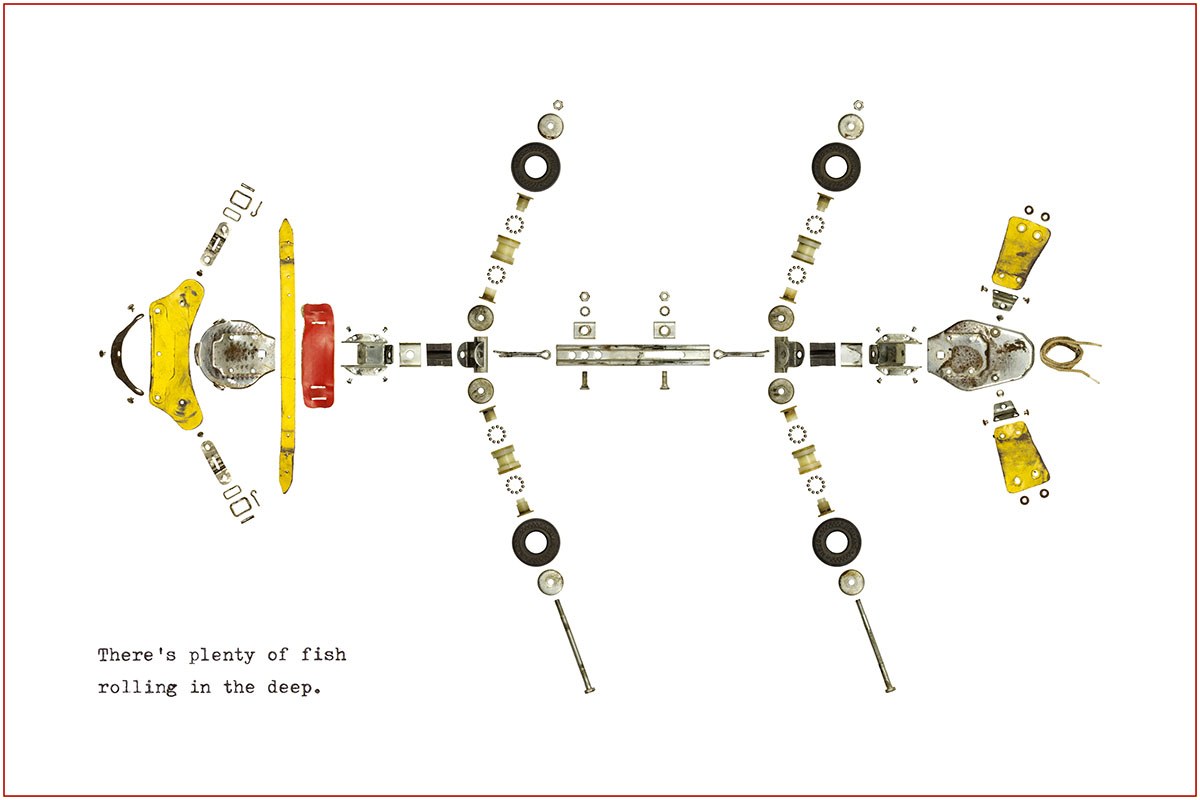
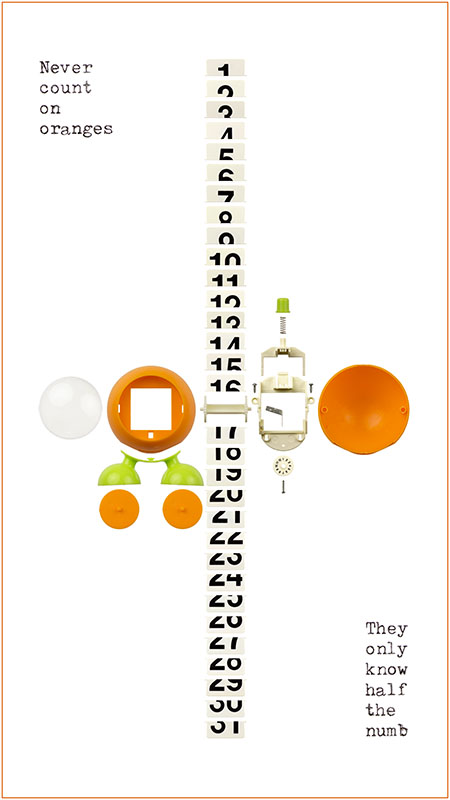This Is How I Roll and Fall

This Is How I Roll and Fall

O dear, it’s gone all figurative! Sometimes dyslectic this happens. I try to be a good deconstructionist and capture the soul of objects in the coldest, most engineeringlike way possible by arranging the parts as close to their relatives as I can. And so I did with this roller skate from Mezo Holland. But sometimes, clinical deconstruction results in a picture of something else altogether, QED. When I was finished, I was staring in the watery eye of a fish. I only tilted the axles a bit to make it more fishy, but otherwise the emergence of this fish was purely accidental.

Confessions:

1) I did cheat on the ball bearing balls. There’s 88 of them. And they’re all pretty much the same. After ten of them I really couldn’t be bothered. Say I’m lazy, say I’m efficient; I’ll call you al big fat liar both times and before you know it, we’re having a big fight. That can’t be right, with Christmas around the corner. So let’s just accept reality for what it is and move on happily and merrily.

2) I did intend to deconstruct both skates, but it turned out some violence was required to persuade the tires to come off the rims. So some tires and some rims were destroyed. But still, it’s better to save one skate than to doom the pair. Or not. I don’t know. Much, I might add.

3) I love Adele.

Numbers time. This roller skate had 179 parts, 88 of which were ball bearing balls. So almost half the parts are clones! I must introduce a new variable, the Clone Score, indicating the number of occurrences of the prevalent part in relation to the total number of parts. This one would obviously score well (Clone Score=.49), but Orange Calendar Man (below) would outscore it with CS=.61 –provided I ignore the printed numbers on the flappy flaps and consider all flappy flaps to be the same.

Final thought (enter Jerry Springer): Note how the majority of parts hardly defines the whole. If you saw a pile of ball bearing balls, you wouldn’t necessarily think: ‘Hey, that’s half a roller skate!’ On the other hand, there wouldn’t be much rolling without those 88 balls.